电子-电子相互作用、量子干涉和无序对输运性质的影响是凝聚态物理研究的一个重要主题。量子干涉的一阶效应包括被广泛研究的弱局域化(weak localization)和反弱局域化(weak antilocalization)效应,分别对应于正交对称性(orthogonal symmetry)和辛对称性(symplectic symmetry)的体系。2004年Minkov等发现,对于前者,比如无序足够强的弱自旋轨道耦合半导体,电子-电子相互作用和量子干涉效应产生的二阶量子修正可强烈地抑制磁电导。然而,对于具有辛对称性的电子系统,如拓扑绝缘体、外尔半金属及强自旋轨道耦合半导体,尚无工作研究二阶或更高阶量子效应如何影响磁电导。
bdy必定赢官网/北京凝聚态物理国家研究中心纳米物理与器件实验室/应用物理中心李永庆研究员指导的博士生史刚、高凡、张仁聪以及光物理实验室的李治林副研究员与以色列巴伊兰大学的Dmitri Gutman教授及德国卡尔斯鲁厄大学的Igor Gornyi研究员合作,对这一问题开展了实验和理论研究。他们利用双栅调控的高质量三维拓扑绝缘体(Bi,Sb)2(Te,Se)3单晶薄片开展了实验研究。在这种器件中,电子输运性质由化学势可大范围调控的表面态狄拉克费米子主导。实验发现,当载流子浓度降低时,磁电导幅度逐渐增强,并在费米能级接近狄拉克点时达到最大值,这与正交对称系统中磁电导随无序增强被逐渐减弱形成鲜明对比。理论分析表明,这一现象可归结为电子-电子相互作用及二阶量子干涉效应导致的磁电导增强。研究还表明,尽管拓扑绝缘体表面态中存在退相干长度、平均自由程、热长度和磁长度等多个尺度的相互竞争,其低场磁电导可以使用推广的Hikami-Larkin-Nagaoka (HLN)公式描述,详细的磁电导分析可以深化对拓扑绝缘体中复杂电子结构的认识,包括局域电荷液团产生的电子屏蔽效应、退相干以及与电子-空穴不对称性。该项工作发表于S. Shi et al., Nature Communications 14, 2596 (2023).
上述研究进展还为理解超薄三维拓扑绝缘体的一个长期令人困惑的输运问题提供了契机。在三维拓扑绝缘体的超薄膜中,上下表面的杂化会改变表面态电子的贝利相位。理论预言随着薄膜厚度的减小,较厚样品中出现的反弱局域化将过渡到超薄膜中的弱局域化,但迄今在实验中很难观察到这一现象。纳米物理与器件实验室的博士生牛雪翻、刘宇新在滕静副研究员和李永庆研究员的指导下,研究了分子束外延生长的(Bi1-xSbx)2Te3的电子输运性质,并可对薄膜的厚度、掺杂水平和化学势等多个参数进行调控。他们发现,在所有实验参数下,垂直磁场中测量的样品磁电导都保持负值,这说明在这些超薄(Bi,Sb)2Te3薄膜中不存在理论预言的全局弱局域化。经分析,这一实验结果可通过样品中存在的长程无序以及电子-电子相互作用和量子干涉产生的二阶量子修正进行解释。研究还表明,拓扑绝缘体超薄膜中的输运性质不仅与具有辛对称性体系中的反弱局域化不同,而且与具有正交对称性体系中出现的弱局域化或弱绝缘体态(weak insulator)迥异。该工作发表于X. F. Niu et al., Physical Review B 107, 115112 (2023).
该项研究得到了国家自然科学基金、科技部国家重点研发计划、bdy必定赢官网先导B类专项的支持。
相关论文链接:
[1] https://www.nature.com/articles/s41467-023-38256-4
[2] https://journals.aps.org/prb/abstract/10.1103/PhysRevB.107.115112
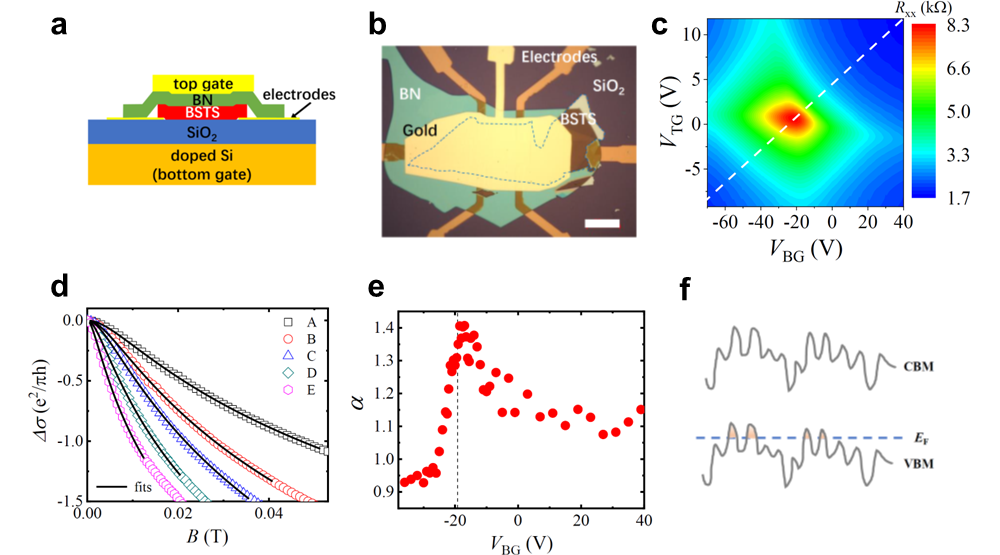
图1 拓扑绝缘体表面态磁电导的量子修正。(a, b)双栅调控拓扑绝缘体(Bi,Sb)2(Te,Se)3器件的侧面示意图及光学俯视图像;(c)纵向电阻Rxx 随顶栅电压(VTG)和底栅电压(VBG )的变化;(d)不同栅压下的代表性磁电导曲线。(e)根据HLN公式拟合得到的前置因子 随栅压的变化,黑色虚线表示费米能级接近狄拉克点; (f)当费米能级接近电荷中心点时,无序导致样品内部空穴液团(hole puddles)的生成。摘自Shi et al., Nat. Commun. 14, 2596 (2023).

图2 超薄拓扑绝缘体中负磁电导的鲁棒性研究。(a)厚度为 2 nm的 (Bi1-xSbx)2Te3薄膜在不同栅压下的磁电导。空心图形为实验数据,实线为HLN拟合结果。(b)考虑长程无序和二阶量子修正后磁电导的数值模拟结果。(c)超薄 (Bi1-xSbx)2Te3中费米能级的调控以及长程无序导致的化学势涨落示意图。(d)不同输运体系的前置因子 对1/g的依赖关系(g为无量纲电导),图中WAL、WL和WI分别表示反弱局域化、弱局域化和弱绝缘体。摘自Niu et al., Phys. Rev. B 107, 115112 (2023).

